Definitions and Formulas
Avogadro’s law states that the volume of any gas is proportional to the amount of gas in moles when the temperature and pressure remain constant. In other words, equal volumes of any gas contain the same number of molecules if the conditions do not change. Note that masses of the different gases will not be the same because they have different molecular masses. A balloon filled with helium will be 33 times lighter than a balloon filled with xenon gas.
A mole is a measure of the quantity of a substance. A mole of a substance is defined as exactly 6.022 140 76 × 10²³ particles (atoms, molecules, ions, or electrons). A mole of a substance measured in grams is numerically equal to the average mass of one molecule of the compound, in unified atomic mass units. For example, one mole of oxygen with an atomic mass of 16 corresponds to 16 grams of this gas. One mole of an ideal gas at standard conditions occupies 22.4 liters. The number 6.022 140 76 × 10²³ is called the Avogadro constant.
A modern statement of Avogadro’s law states:
For a given mass of an ideal gas, its volume and amount in moles are directly proportional if the temperature and pressure maintained constant.
According to Avogadro’s law, Volume of the gas will be directionally proportional to the amount of moles of the gas at constant temperature and constant pressure. We can also say that if amount of moles of gas will be increased then according to Avogadro’s law, volume of the gas will also be increased. According to Avogadro's law, the volume of a gas A) depends only on the number of moles in the sample. B) is directly related to the number of moles at constant temperature and pressure. C) is inversely related to the number of moles at constant temperature and pressure. According to Avogadro's law, the volume of a gas will as the is increased while the are held constant. A) increase; number of moles; pressure and temperature B) decreased; number of moles; pressure and temperature C) increase; temperature; pressure and number of moles D) decrease; pressure; temperature and number of moles E) increase; pressure; temperature and number of moles.
Mathematically, the law can be written as
or
where k is a constant depending on a given pressure and temperature. This means the ideal gas constant is the same for all gases.
If we consider the pairing of variables at different states (initial and final) of the same process, we can write a proportion:
where V is the volume, n is the amount of substance in moles and the subscripts 1 and 2 refer to the initial and final states of a gas in a system. Any unknown term of this proportion can be found by means of cross-multiplication. For example, to find the initial volume V1, we will write
History
An Italian scientist Amedeo Avogadro is best known for the Avogadro constant or Avogadro number, which only bears his name and was proposed by a French scientist Jean Perrin in 1909 and first calculated by an Austrian chemist and physicist Joseph Loschmidt (1865) and later by James Clerk Maxwell (1873). Unlike the Avogadro’s constant, Avogadro’s law was actually proposed by Amedeo Avogadro. It was the fourth empirical gas law and was published in 1811 after Boyle’s law (1662), Charles’s law (1787), and Gay-Lussac’s law (1808). Textbooks in French call this law La loi d'Avogadro-Ampère because it was independently formulated by a French scientist André-Marie Ampère in 1814.
It is noteworthy that during Avogadro’s lifetime, the discovery of his law went unnoticed due to criticism from influential chemists of that era — a Swedish chemist Jöns Jacob Berzelius and an English chemist John Dalton. They denied the possibility of the existence of diatomic molecules of simple substances. Only in 1860, the Karlsruhe Congress (the first international congress of chemistry) recognized the role of Avogadro.
Avogadro’s law, which is also called Avogadro’s principle or Avogadro’s hypothesis, only approximates the behavior of real gases because it applies only to an ideal gas. Real gases behave like an ideal gas only under conditions of low temperatures and pressures. At high temperatures and pressures, real gases do not behave in accordance with Avogadro’s law. Also, lighter gas particles of hydrogen, helium yield better results than heavier molecules.
Examples of Avogadro’s Law in Real Life Situations
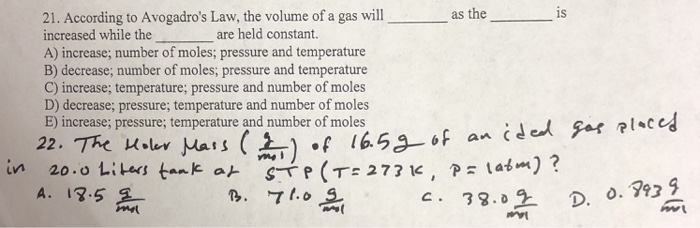
Aerodynamics and Meteorology: Humid Air is Less Dense than Dry Air
Avogadro’s law is of great importance in aerodynamics with reference to engine thrust and wing lift. Dry air consists mostly of nitrogen and oxygen molecules, which weigh more than water molecules. This means that a given volume of moist air is lighter than the same volume of dry air. This is because lighter water vapor molecules present in the humid air “push out” oxygen molecules. At the same time, the number of molecules in a given volume of gas at the same temperature and pressure is the same regardless of its humidity. Humid air with water is less dense than dry air and consequently, it produced less wing lift force and less engine thrust. In conclusion, we have to note that this difference in density seems to be counterintuitive to many people (water is heavier than air!).
Air Balloons
Hydrogen and Helium balloons
Both hydrogen and helium gases are used in toy and weather balloons. They have the same temperature as surrounding air, almost the same pressure, and according to Avogadro’s law, the same number of molecules. At the same time, helium and hydrogen balloons can float because helium molecules and hydrogen atoms are much lighter than molecules of nitrogen and oxygen.
Hot Air Balloons
Hot air balloons float because the air in them is hotter than the air surrounding them. This hot air contains fewer molecules compared to the same volume of the surrounding air. The temperature and pressure of the air inside and outside the balloon are approximately the same and the balloon flotation is due to it has fewer molecules of gases in the air and thus it is lighter than the surrounding air.
Avogadro's Law Calculator
A Ball
When you blow up a ball, its volume increases because you add more molecules. When, however, its valve is not working properly, some of the air leaks our and its volume decreases.
Lungs
Our body needs oxygen to live. It needs oxygen for thinking, moving, digesting food, and all other biochemical processes. When these processes happen, living tissues need oxygen for oxidation, which, in turn, is primarily used for rendering energy that is used for useful purposes. Carbon dioxide is produced as a waste product of this oxidation processes.
Our body needs ventilation to remove carbon dioxide and provide oxygen. Breathing (or ventilation) is the process of moving air into our lungs and out of them to provide gas exchange, which is mostly bringing in oxygen and removing carbon dioxide. When we breathe, inhaled air contains by volume 21% oxygen, 78% nitrogen, and very small amounts of other gases including carbon dioxide, water vapor, and noble gases. The exhaled gas contains by volume up to 5% of carbon dioxide, which is about a 100-fold increase over the inhaled amount of carbon dioxide.
We breathe because of Avogadro’s and other gas laws. When we inhale air (this is called inspiration), our lungs expand and more gas molecules enter them. When we exhale (this is called expiration), their volume decreases, and waste gas molecules are expelled. Our lungs cannot inflate by themselves because they do not have muscles. They expand during inhaling only when the volume of the thoracic cavity is increased through the contraction of:
Avogadro's Gas Law
- the thoracic diaphragm and
- intercostal muscles, which pull the rib cage outwards and upwards.
The thoracic diaphragm is a sheet muscle that separates the thoracic cavity containing lungs and heart from the abdominal cavity containing the stomach, liver, kidneys, small and large intestine, and other organs. During exhaling, the diaphragm and the intercostal muscles relax and the volume of the thoracic cavity is decreased.
The lung capacity of an average adult male is about 6 liters of air. Taller, fit people and those who live at higher altitudes have higher lung volume and shorter, obese people, and those who live at lower altitudes have smaller lung volume. Athletes have the largest lung capacity up to 12 liters. During quiet breathing, the air moved into and out of the lungs called the tidal volume is relatively small — only about 0.5 L in healthy men and 0.4 L in healthy women. At the end of each exhalation, the adult male lungs still contain 2.4 L of air, and female lungs contain 1.8 L of air. This volume is called a functional residual capacity (FRC).
It is interesting to determine how many moles and grams of air we take in and out for every respiratory cycle and what is the pressure difference that is involved in breathing. We will calculate the pressure difference that is necessary for the quiet breathing of a healthy male adult at room temperature and normal atmospheric pressure. To do this, we will use several of our calculators of ideal gas laws.
According To Avogadro's Law The Volume Of A Gas
The amount of air in moles in the lungs before inhaling (FRC) is 2.4 L at 37 °C at the normal atmospheric pressure of 100 kPa is calculated using the ideal gas law (click to view the calculation in the calculator):
As we mentioned before, the tidal volume for quiet breathing in healthy men is 0.5 L. Using the Ideal Gas Calculator, we determine the amount of 0.5L of air in moles at 100 kPa and 20 °С (click to view the calculation in the calculator):
The molar mass of air is 29 g/mol, therefore the calculator shows that 0.021 mole corresponds to 0.6 g of air. Not very much, but this quantity of air in every breath is just enough to keep our body alive and well.
According To Avogadro's Law The Volume Of Gas
The temperature of the air in the lungs is 37 °C, the pressure at the end of the inspiration is the same as atmospheric pressure, therefore, according to Charles’s law, the volume of the air that entered the lungs will change to
(click to view the calculation in the calculator). The total volume of the air in the lungs of at the end of inhaling
Now we have all data to determine the pressure difference necessary for inhaling:
| Air in the Lungs Characteristics | Before Inhaling | After Inhaling |
|---|---|---|
| Pressure of air in kPa (Pa) | 100 | To be determined |
| Temperature of air, in °C (K) | 37 (310,15) | 37 (310,15) |
| Volume of air in L (m³) | 2,4 (0,0024) | 2,929 (0,002929) |
| Quantity of air in moles | 0,093 | 0,093 + 0,021 = 0,114 |
Let us determine the pressure at the start of inhaling that is necessary to inhale 0.5 L of air at 20 °C. According to the ideal gas law,
(click to view the calculation in the calculator). The pressure difference is 100.367 – 100 = 0.367 kPa = 2.75 torr = 2.75 mm Hg = 3.74 cm H2O. This is the pressure difference between the air inside the lungs and atmospheric pressure that is necessary to inhale 0.5 L of air at normal conditions. Recall that this pressure difference is provided by the contraction of the thoracic diaphragm and intercostal muscles.

Comments are closed.